TEOREMA DEL RESTO
En álgebra el teorema del resto afirma que el resto  , que resulta al dividir un polinomio
, que resulta al dividir un polinomio 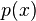 entre
entre  , es igual a
, es igual a 
 , que resulta al dividir un polinomio
, que resulta al dividir un polinomio 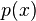 entre
entre  , es igual a
, es igual a 
Esto se deduce directamente de una de las propiedades de la división, la que dice que
donde 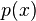 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto y verificándose además, que el grado de
el resto y verificándose además, que el grado de  es menor que el grado de
es menor que el grado de  .
.
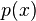 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto y verificándose además, que el grado de
el resto y verificándose además, que el grado de  es menor que el grado de
es menor que el grado de  .
.
En efecto, si tomamos el divisor  entonces
entonces  tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar r, y la fórmula anterior se convierte en:
tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar r, y la fórmula anterior se convierte en:
 entonces
entonces  tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar r, y la fórmula anterior se convierte en:
tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar r, y la fórmula anterior se convierte en:
Tomando el valor  se obtiene que:
se obtiene que:
 se obtiene que:
se obtiene que:
El teorema del resto nos permite calcular  calculando el resto o viceversa. También puede deducirse de él, fácilmente, el teorema del factor, de gran utilidad para descomponer un polinomio en factores.
calculando el resto o viceversa. También puede deducirse de él, fácilmente, el teorema del factor, de gran utilidad para descomponer un polinomio en factores.
 calculando el resto o viceversa. También puede deducirse de él, fácilmente, el teorema del factor, de gran utilidad para descomponer un polinomio en factores.
calculando el resto o viceversa. También puede deducirse de él, fácilmente, el teorema del factor, de gran utilidad para descomponer un polinomio en factores.Ejemplo
Sea  .
.
 .
.
Al dividir 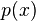 por
por  obtenemos el cociente
obtenemos el cociente
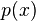 por
por  obtenemos el cociente
obtenemos el cociente y el resto
y el resto  .
.
Podemos asegurar entonces, que  .
.
 .
.Teorema del factor
Una consecuencia directa es que 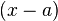 es un factor del polinomio
es un factor del polinomio  si y sólo si
si y sólo si  .
.
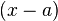 es un factor del polinomio
es un factor del polinomio  si y sólo si
si y sólo si  .
.


No hay comentarios.:
Publicar un comentario