INTERVALOS DE NUMEROS REALES
Un intervalo es un subconjunto  ℝ. A tal subconjunto se le exige que para cualesquiera
ℝ. A tal subconjunto se le exige que para cualesquiera  y todo
y todo  con
con  se satisfaga que
se satisfaga que  . 2Específicamente, un intervalo real es un subconjunto conexo de la recta real
. 2Específicamente, un intervalo real es un subconjunto conexo de la recta real  . Es un conjunto Un intervalo
. Es un conjunto Un intervalo  es una parte de
es una parte de  que verifica la siguiente propiedad:
que verifica la siguiente propiedad:
Si  y  son elementos de  con  , entonces para todo  tal que  , se cumple que 
|
.
Notación
Intervalo abierto
No incluye los extremos.
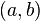 o bien
o bien ![]a,b[\](https://upload.wikimedia.org/math/9/7/d/97d6ce8ff7d3fd1e5118d1e042bfc856.png)
- Notación conjuntista o en términos de desigualdades:


En la topología usual de la recta (o

) se usa un intervalo abierto para definir un conjunto abierto en dicha topología. En la topología usual de

, un intervalo abierto es un conjunto abierto. El intervalo abierto (a, b) es igual a su interior, su frontera es el conjunto {a, b} y su clausura es el intervalo cerrado [a, b].
4 No tiene puntos aislados, mientras que todos su puntos son puntos de acumulación del mismo intervalo.
5
Intervalo cerrado
Sí incluye los extremos.
- Que se indica:
![I = [a,b]\](https://upload.wikimedia.org/math/5/a/6/5a6aef6ce626a63d1e3c1cfb17e1a97e.png)
En notación conjuntista:
![I = [a,b] \Leftrightarrow](https://upload.wikimedia.org/math/3/9/5/3957983450d57e02263ced14a146807f.png)

Si incluye únicamente uno de los extremos.
- Con la notación
![(a,b]\](https://upload.wikimedia.org/math/e/1/0/e105896da1efd4783135a0dacd11b9b8.png) o bien
o bien ![]a,b]\](https://upload.wikimedia.org/math/d/f/1/df16e2650d45bf0cf8f502373865a272.png) indicamos.
indicamos.
En notación conjuntista:
![I = (a,b]\Leftrightarrow](https://upload.wikimedia.org/math/2/5/b/25b80efa2a22fe02797857cace2a3511.png)

- Y con la notación
 o bien
o bien 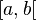 ,
,
En notación conjuntista:


Los cuatro tipos de intervalos anteriores se llaman
finitos; los expertos asignan como su longitud |b- a|. Son muy útiles en el análisis matemático y en los temas de topología general, para el estudio de diferentes conceptos como clausura, interior, frontera, conexidad, etc.
6 Se usan en definición de funciones como la función máximo entero, o la función techo o función piso en matemáticas discretas y para la solución de ecuaciones que conllevan valor abosoluto, la función signo, etc.
7
Los intervalos finitos tienen un centro de simetría que es (a + b)/2, llamado
punto medio, donde los extremos son a y b con a < b. En el caso a=b, no existe punto medio y el intervalo abierto es ∅.
8
Intervalo infinito
Incluye un extremo e infinito por la derecha.
- Con la notación
 indicamos.
indicamos.
En notación conjuntista:


Sin incluir el extremo:
- Y con la notación
 ,
,


Incluye un extremo e infinito por la izquierda.
- Con la notación
![(-\infty, a]\](https://upload.wikimedia.org/math/0/7/b/07bb1e1c13ff67945983bf469caffc2e.png) indicamos.
indicamos.
En notación conjuntista:
![I = (-\infty, a]\Leftrightarrow](https://upload.wikimedia.org/math/d/7/a/d7a04e05c0fadcf21a9cf2995aec3274.png)

Sin incluir el extremo:
- Y con la notación
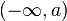 ,
,
En notación conjuntista:


Para todo valor real:
- Y con la notación
 ,
,
En notación conjuntista:


Familia de intervalos
Operaciones con intervalos
En notación conjuntista: supongamos el conjunto A:

Esto se lee: A es el conjunto de todos los números reales x tal que x es menor que cuatro.
Y el conjunto B:

B es el conjunto de todos los números reales x, tal que 9 es menor que cualquier x .
El conjunto unión de A y B sería:
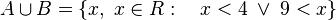
O también se puede anotar:

Un elemento está en la unión de dos o más conjuntos s.s.s. está por lo menos en uno de ellos.
El conjunto intersección de
A y
B no existe
9 :
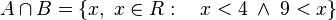
porque A y B no tienen puntos en común.
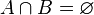
Definido el conjunto C:

Es decir, que el conjunto C toma valores entre -3 y 15, siempre siendo x un número real.
El conjunto intersección de A y C es:
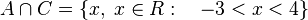
El conjunto intersección es aquel que toma los valores en común entre todos los conjuntos incluidos.
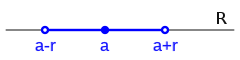
Entorno simétrico
Un entorno simétrico o entorno de centro a y radio r se representa:
- Con la notación
 indicamos.
indicamos.


Entorno reducido
Un entorno reducido de centro a y radio r se representa:
- Con la notación
 indicamos.
indicamos.
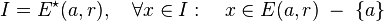
Un
entorno reducido de un punto
p es un entorno de
p, menos {
p}. Por ejemplo, el intervalo (−1, 1) = {
y: −1 <
y < 1} es un entorno de
p = 0 en la
recta real, entonces el conjunto (−1, 0) ∪ (0, 1) = (−1, 1) − {0} es un entorno reducido de 0.
Nota
Ejemplos gráficos[editar]
|
|
Transformación lineal de intervalos.
|
|
|
Transformación lineal de intervalos.
|
|
Clasificación
Se pueden clasificar los intervalos según sus características
topológicas (intervalos abiertos, cerrados, semiabiertos) o según sus características
métricas (longitud: nula, finita no nula, infinita).
La siguiente tabla resume los 11 casos posibles, con a ≤ b, y x perteneciente al intervalo:
| Notación | Intervalo | Longitud | Descripción |
|---|
![[a, b] \,](https://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png) | 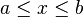 | 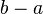 | Intervalo cerrado de longitud finita. |
 | 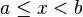 | 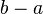 | Intervalo semiabierto (cerrado en a, abierto en b). |
![]a, b] \ \ \mathrm{ \acute o } \ \ (a, b] \!](https://upload.wikimedia.org/math/0/1/8/0189f84b7a0ea78dbc527c545d8c9598.png) |  | 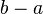 | Intervalo semiabierto (abierto en a, cerrado en b). |
![]a, b[ \ \ \mathrm{ \acute o } \ \ (a, b) \!](https://upload.wikimedia.org/math/1/0/d/10d97baef8714cd0982a87681cfe4d1f.png) | 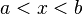 | 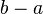 | Intervalo abierto. |
![]-\infty, b[ \ \ \mathrm{ \acute o } \ \ (- \infty, b) \!](https://upload.wikimedia.org/math/0/9/7/097e7c70e6cbf2559d82fcb85f853033.png) | 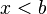 |  | Intervalo semiabierto. |
![]-\infty, b] \ \ \mathrm{ \acute o } \ \ (- \infty, b] \!](https://upload.wikimedia.org/math/e/8/2/e82cc38f6052cb558df6d0be418c5659.png) | 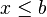 |  | Intervalo semiabierto. |
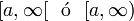 | 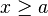 |  | Intervalo semiabierto. |
![]a, \infty [ \ \ \mathrm{ \acute o } \ \ (a, \infty ) \!](https://upload.wikimedia.org/math/8/e/6/8e62b6ce3cbde6646d2cd2dda6a5b6bc.png) |  |  | Intervalo semiabierto. |
![]\infty, + \infty [ \ \ \mathrm{ \acute o } \ \ (\infty, + \infty ) \!](https://upload.wikimedia.org/math/6/b/a/6ba8dc9071eaad7acf515f333bba45cf.png) | 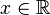 |  | Intervalo a la vez abierto y cerrado. |
 |  | 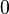 | Intervalo cerrado de longitud nula (intervalo degenerado). |
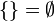 | sin elemento | cero | Conjunto vacíoIntervalo abierto (a,a). |
Caracterización
Intervalo cerrado
El número real
x está en
![I= [a, b] \,](https://upload.wikimedia.org/math/0/3/5/035b124a5293349ceeb7ce956a7646cc.png)
si sólo si
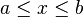
. Los puntos
a y
b son elementos del intervalo cerrado
I;
aes el ínfimo y
b el supremo. El intervalo cerrado es la clausura del intervalo abierto y los semiabiertos con extremos
a y
b con
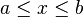
. El intervalo abierto

es el interior del intervalo cerrado de extremos a y b; y estos puntos son los únicos que están en la frontera del intervalo cerrado
![I= [a, b] \,](https://upload.wikimedia.org/math/0/3/5/035b124a5293349ceeb7ce956a7646cc.png)
; este es un conjunto cerrado y compacto con la topología usual de la recta .
11
Propiedades
- La intersección de intervalos de
 es también un intervalo.
es también un intervalo.
- La unión de intervalos de
 no siempre es un intervalo (lo será si la intersección es no vacía).
no siempre es un intervalo (lo será si la intersección es no vacía).
- Los conjuntos conexos de
 son exactamente los intervalos.12
son exactamente los intervalos.12
- Los intervalos cerrados sobre una recta se denominan «segmento de recta», son conjuntos cerrados según la topología usual, conexos y compactos.13
- La imagen por una función continua de un intervalo de
 es un intervalo de
es un intervalo de  . Esta es una formulación delTeorema del valor intermedio.
. Esta es una formulación delTeorema del valor intermedio.
- Según la topología usual de ℝ, un conjunto abierto es la unión de intervalos abiertos.14
Aritmética de intervalos
Sean I = [a, b] y J = [c, d] con a ≤ x ≤ b, y c ≤ y ≤ d.
Entonces: a + c ≤ x + y ≤ b + d. Lo que justifica que
- I + J = [ a + c, b + d ].
- I - J = [ a - d, b - c ].
- Si se toman a, b, c y d positivos no nulos, I · J = [ ac, bd ] y I / J = [ a/d, b/c ].
Generalización
Un intervalo
n-dimensional se define como un subconjunto de

, que es el
producto cartesiano de
n intervalos:

, uno en cada eje de coordenadas......

Entorno de centro
a y radio ε.
En términos
topológicos, en el
espacio métrico 
usual los intervalos son las
bolas abiertas y cerradas. De manera más general, se le llama
vecindad o
entorno de centro
a y radio ε, al conjunto de puntos
x cuya distancia a
a es menor que ε.

medible y tiene la misma cardinalidad de la recta real.3
 , que resulta al dividir un polinomio
, que resulta al dividir un polinomio 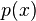 entre
entre  , es igual a
, es igual a 
 , que resulta al dividir un polinomio
, que resulta al dividir un polinomio 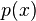 entre
entre  , es igual a
, es igual a 
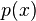 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto y verificándose además, que el grado de
el resto y verificándose además, que el grado de  es menor que el grado de
es menor que el grado de  .
.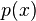 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto y verificándose además, que el grado de
el resto y verificándose además, que el grado de  es menor que el grado de
es menor que el grado de  .
. entonces
entonces  tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar r, y la fórmula anterior se convierte en:
tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar r, y la fórmula anterior se convierte en: entonces
entonces  tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar r, y la fórmula anterior se convierte en:
tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar r, y la fórmula anterior se convierte en: se obtiene que:
se obtiene que: se obtiene que:
se obtiene que: calculando el resto o viceversa. También puede deducirse de él, fácilmente, el teorema del factor, de gran utilidad para descomponer un polinomio en factores.
calculando el resto o viceversa. También puede deducirse de él, fácilmente, el teorema del factor, de gran utilidad para descomponer un polinomio en factores. calculando el resto o viceversa. También puede deducirse de él, fácilmente, el teorema del factor, de gran utilidad para descomponer un polinomio en factores.
calculando el resto o viceversa. También puede deducirse de él, fácilmente, el teorema del factor, de gran utilidad para descomponer un polinomio en factores. .
. .
.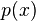 por
por  obtenemos el cociente
obtenemos el cociente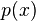 por
por  obtenemos el cociente
obtenemos el cociente y el resto
y el resto  .
. .
. .
.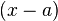 es un factor del polinomio
es un factor del polinomio  si y sólo si
si y sólo si  .
.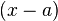 es un factor del polinomio
es un factor del polinomio  si y sólo si
si y sólo si  .
.









 y
y  son elementos de
son elementos de  , entonces para todo
, entonces para todo  tal que
tal que  , se cumple que
, se cumple que 

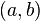 o bien
o bien ![]a,b[\](https://upload.wikimedia.org/math/9/7/d/97d6ce8ff7d3fd1e5118d1e042bfc856.png)



![I = [a,b]\](https://upload.wikimedia.org/math/5/a/6/5a6aef6ce626a63d1e3c1cfb17e1a97e.png)
![I = [a,b] \Leftrightarrow](https://upload.wikimedia.org/math/3/9/5/3957983450d57e02263ced14a146807f.png)


![(a,b]\](https://upload.wikimedia.org/math/e/1/0/e105896da1efd4783135a0dacd11b9b8.png) o bien
o bien ![]a,b]\](https://upload.wikimedia.org/math/d/f/1/df16e2650d45bf0cf8f502373865a272.png) indicamos.
indicamos.![I = (a,b]\Leftrightarrow](https://upload.wikimedia.org/math/2/5/b/25b80efa2a22fe02797857cace2a3511.png)


 o bien
o bien 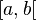 ,
,


 indicamos.
indicamos.


 ,
,


![(-\infty, a]\](https://upload.wikimedia.org/math/0/7/b/07bb1e1c13ff67945983bf469caffc2e.png) indicamos.
indicamos.![I = (-\infty, a]\Leftrightarrow](https://upload.wikimedia.org/math/d/7/a/d7a04e05c0fadcf21a9cf2995aec3274.png)


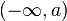 ,
,


 ,
,




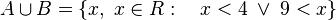


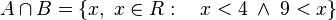
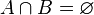


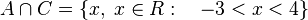
 indicamos.
indicamos.


 indicamos.
indicamos.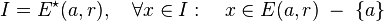
 ) para indicar que no hay cota.
) para indicar que no hay cota.


![[a, b] \,](https://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png)
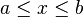
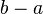

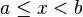
![]a, b] \ \ \mathrm{ \acute o } \ \ (a, b] \!](https://upload.wikimedia.org/math/0/1/8/0189f84b7a0ea78dbc527c545d8c9598.png)

![]a, b[ \ \ \mathrm{ \acute o } \ \ (a, b) \!](https://upload.wikimedia.org/math/1/0/d/10d97baef8714cd0982a87681cfe4d1f.png)
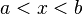
![]-\infty, b[ \ \ \mathrm{ \acute o } \ \ (- \infty, b) \!](https://upload.wikimedia.org/math/0/9/7/097e7c70e6cbf2559d82fcb85f853033.png)
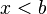
![]-\infty, b] \ \ \mathrm{ \acute o } \ \ (- \infty, b] \!](https://upload.wikimedia.org/math/e/8/2/e82cc38f6052cb558df6d0be418c5659.png)
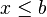
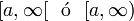
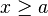
![]a, \infty [ \ \ \mathrm{ \acute o } \ \ (a, \infty ) \!](https://upload.wikimedia.org/math/8/e/6/8e62b6ce3cbde6646d2cd2dda6a5b6bc.png)

![]\infty, + \infty [ \ \ \mathrm{ \acute o } \ \ (\infty, + \infty ) \!](https://upload.wikimedia.org/math/6/b/a/6ba8dc9071eaad7acf515f333bba45cf.png)
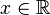


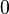
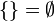
![I= [a, b] \,](https://upload.wikimedia.org/math/0/3/5/035b124a5293349ceeb7ce956a7646cc.png) si sólo si
si sólo si  es el interior del intervalo cerrado de extremos a y b; y estos puntos son los únicos que están en la frontera del intervalo cerrado
es el interior del intervalo cerrado de extremos a y b; y estos puntos son los únicos que están en la frontera del intervalo cerrado  , que es el
, que es el  , uno en cada eje de coordenadas......
, uno en cada eje de coordenadas......
