POLINOMIOS
En matemáticas, un polinomio y este del griego ‘ ‘regla’, ‘prescripción’, ‘distribución’)1 2 3 es una expresión matemática constituida por un conjunto finito de variables (no determinadas o desconocidas) y constantes (números fijos llamados coeficientes), utilizando únicamente las operaciones aritméticas de suma, resta y multiplicación, así como también exponentes enteros positivos. En términos más precisos, es unarelación n-aria de monomios, o una sucesión de sumas y restas de potencias enteras de una o de varias variables indeterminadas.
Es frecuente el término polinómico (ocasionalmente también el anglicismo polinomio), como adjetivo, para designar cantidades que se pueden expresar como polinomios de algún parámetro, como por ejemplo: tiempo polinómico
Los polinomios son objetos muy utilizados en matemáticas y en ciencia. En la práctica, son utilizados en cálculo y análisis matemático para aproximar cualquier función derivable; las ecuaciones polinómicas y las funciones polinómicas tienen aplicaciones en una gran variedad de problemas, desde la matemática elemental y el álgebra
Polinomios de una variable[editar]
Para a0, …, an constantes en algún anillo A (en particular podemos tomar un cuerpo, como  o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y  , entonces un polinomio
, entonces un polinomio  de grado n en la variable x es un objeto de la forma
de grado n en la variable x es un objeto de la forma
 o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y  , entonces un polinomio
, entonces un polinomio  de grado n en la variable x es un objeto de la forma
de grado n en la variable x es un objeto de la forma
Representado como:

el polinomio se puede escribir más concisamente usando sumatorios como:
Las constantes a0, …, an se llaman los coeficientes del polinomio. A a0 se le llama el coeficiente constante (o término independiente) y a an, el coeficiente principal. Cuando el coeficiente principal es 1, al polinomio se le llama mónico o normalizado.
Polinomios de varias variables
Como ejemplo de polinomios de dos variables, desarrollando los binomios:
(2)
Para obtener la expansión de las potencias de una resta (véase productos notables), basta con tomar -y en lugar de y en el caso anterior. La expresión (2) queda de la siguiente forma:
Los polinomios de varias variables, a diferencia de los de una variable, tienen en total más de una variable. Por ejemplo los monomios:
En detalle el último de ellos 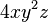 es un monomio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.
es un monomio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.
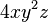 es un monomio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.
es un monomio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.Grado de un polinomio[editar]
Se define el grado de un monomio como el exponente de su variable. El grado de un polinomio es el del monomio de mayor grado.
- Ejemplos
- P(x) = 2, polinomio de grado cero (el polinomio solo consta del término independiente).
- P(x) = 3x + 2, polinomio de grado uno.
- P(x) = 3x² + 2x, polinomio de grado dos.
- P(x) = 2x3+ 3x + 2, polinomio de grado tres.
- P(x) = 4x4+ 4x + 2, polinomio de grado cuatro.
- P(x) = 2x5+ 3x + 1, polinomio de grado cinco.
Convencionalmente se define el grado del polinomio nulo como  .
.
 .
.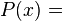

![P(x) \in K[x]](https://upload.wikimedia.org/math/3/f/9/3f903d25c00c40ac2d0e70d5efd4f99e.png) no es más que una
no es más que una  tal que
tal que  .
.
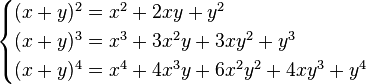
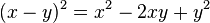

No hay comentarios.:
Publicar un comentario